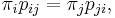Time reversibility
Time reversibility is an attribute of some stochastic processes and some deterministic processes.
If a stochastic process is time reversible, then it is not possible to determine, given the states at a number of points in time after running the stochastic process, which state came first and which state arrived later.
If a deterministic process is time reversible, then the time-reversed process satisfies the same dynamical equations as the original process, AKA reversible dynamics; the equations are invariant or symmetric under a change in the sign of time. Classical mechanics and optics are both time-reversible. Modern physics is not quite time-reversible; instead it exhibits a broader symmetry, CPT symmetry.
Time reversibility generally occurs when, within a process, it can be broken up into sub-processes which undo the effects of each other. For example, in phylogenetics, a time-reversible nucleotide substitution model such as the generalised time reversible model has the total overall rate into a certain nucleotide equal to the total rate out of that same nucleotide.
Time Reversal, specifically in the field of acoustics, is a process by which the linearity of sound waves is used to reverse a received signal; this signal is then re-emitted and a temporal compression occurs, resulting in a reverse of the initial excitation waveform being played at the initial source. Mathias Fink is credited with proving Acoustic Time Reversal by experiment.
Contents |
Stochastic processes
A formal definition of time-reversibility is stated by Tong[1] in the context of time-series. In general, a Gaussian process is time-reversible. The process defined by a time-series model which represents values as a linear combination of past values and of present and past innovations (see Autoregressive moving average model) is, except for limited special cases, not time-reversible unless the innovations have a normal distribution (in which case the model is a Gaussian process).
A stationary Markov Chain is reversible if the transition matrix {pij} and the stationary distribution {πj} satisfy
for all i and j.[2] Such Markov Chains provide examples of stochastic processes which are time-reversible but non-Gaussian.
See also
Notes
References
-
- Isham, V. (1991)Modelling stochastic phenomena. In: Stochastic Theory and Modelling", Hinkley, DV., Reid, N., Snell, E.J. (Eds). Chapman and Hall. ISBN 0-412-30390-9.
- Tong, H. (1990) Non-linear Time Series: A Dynamical System Approach. Oxford UP. ISBN 0-19-852300-9